热线电话:0755-23712116
邮箱:contact@shuangyi-tech.com
地址:深圳市宝安区沙井街道后亭茅洲山工业园工业大厦全至科技创新园科创大厦2层2A
从机器视觉的角度,由简入繁从相机标定,平面物体检测、有纹理物体、无纹理物体、深度学习、与任务/运动规划结合等6个方面深度解析文章的标题。
首先,我们要了解,机器人领域的视觉(Machine Vision)跟计算机领域(Computer Vision)的视觉有一些不同:机器视觉的目的是给机器人提供操作物体的信息。所以,机器视觉的研究大概有这几块:
1. 物体识别(Object Recognition):在图像中检测到物体类型等,这跟 CV 的研究有很大一部分交叉;
2. 位姿估计(Pose Estimation):计算出物体在摄像机坐标系下的位置和姿态,对于机器人而言,需要抓取东西,不仅要知道这是什么,也需要知道它具体在哪里;
3. 相机标定(Camera Calibration):因为上面做的只是计算了物体在相机坐标系下的坐标,我们还需要确定相机跟机器人的相对位置和姿态,这样才可以将物体位姿转换到机器人位姿。
当然,我这里主要是在物体抓取领域的机器视觉;SLAM 等其他领域的就先不讲了。
由于视觉是机器人感知的一块很重要内容,所以研究也非常多了,我就我了解的一些,按照由简入繁的顺序介绍吧。
一. 相机标定
这其实属于比较成熟的领域。由于我们所有物体识别都只是计算物体在相机坐标系下的位姿,但是,机器人操作物体需要知道物体在机器人坐标系下的位姿。所以,我们先需要对相机的位姿进行标定。
内参标定就不说了,参照张正友的论文,或者各种标定工具箱;
外参标定的话,根据相机安装位置,有两种方式:
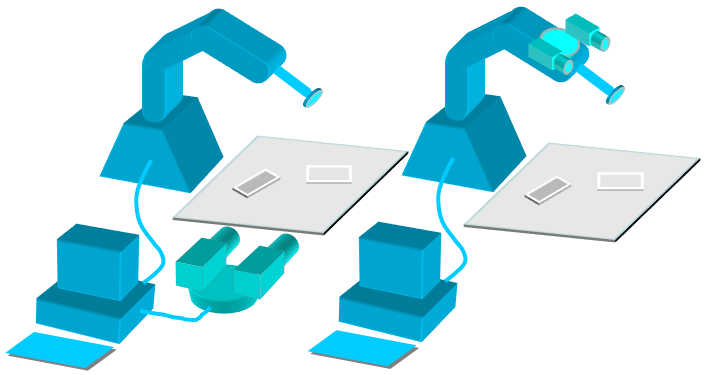
Eye to Hand:相机与机器人极坐标系固连,不随机械臂运动而运动
Eye in Hand:相机固连在机械臂上,随机械臂运动而运动
两种方式的求解思路都类似,首先是眼在手外(Eye to Hand)
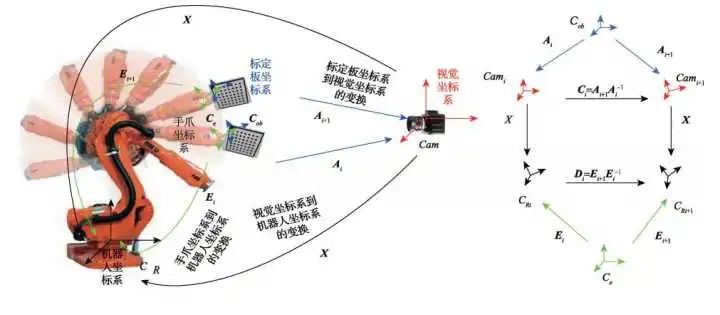
只需在机械臂末端固定一个棋盘格,在相机视野内运动几个姿态。由于相机可以计算出棋盘格相对于相机坐标系的位姿A_i 、机器人运动学正解可以计算出机器人底座到末端抓手之间的位姿变化E_i 、而末端爪手与棋盘格的位姿相对固定不变。
这样,我们就可以得到一个坐标系环 CX=XD
这种结构的求解有很多方法,这边给出一个参考文献:
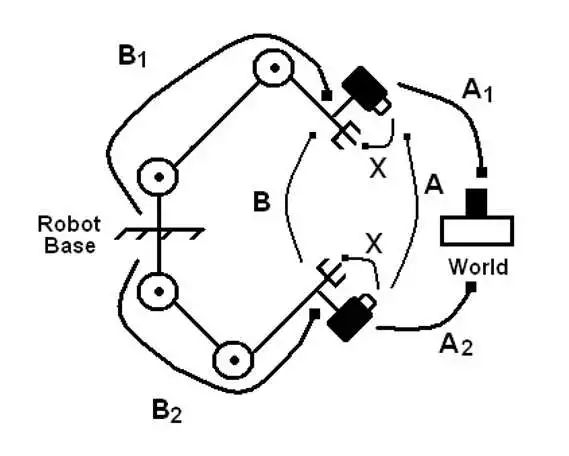
Shiu, Yiu Cheung, and Shaheen Ahmad. "Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX= XB."ieee Transactions on Robotics and Automation 5.1 (1989): 16-29.
而对于眼在手上(Eye in Hand)的情况,也类似,在地上随便放一个棋盘格(与机器人基座固连),然后让机械臂带着相机走几个位姿,然后也可以形成一个AX=XB 的坐标环。
二. 平面物体检测
这是目前工业流水线上最常见的场景。目前来看,这一领域对视觉的要求是:快速、精确、稳定。所以,一般是采用最简单的边缘提取+边缘匹配/形状匹配的方法;而且,为了提高稳定性、一般会通过主要打光源、采用反差大的背景等手段,减少系统变量。

目前,很多智能相机都直接内嵌了这些功能;而且,物体一般都是放置在一个平面上,相机只需计算物体的(x,y,θ)T 三自由度位姿即可。
另外,这种应用场景一般都是用于处理一种特定工件,相当于只有位姿估计,而没有物体识别。
当然,工业上追求稳定性无可厚非,但是随着生产自动化的要求越来越高,以及服务类机器人的兴起。对更复杂物体的完整位姿(x,y,z,rx,ry,rz)T 估计也就成了机器视觉的研究热点。

三.有纹理的物体
机器人视觉领域是最早开始研究有纹理的物体的,如饮料瓶、零食盒等表面带有丰富纹理的都属于这一类。
当然,这些物体也还是可以用类似边缘提取+模板匹配的方法。但是,实际机器人操作过程中,环境会更加复杂:光照条件不确定(光照)、物体距离相机距离不确定(尺度)、相机看物体的角度不确定(旋转、仿射)、甚至是被其他物体遮挡(遮挡)。

幸好有一位叫做 Lowe 的大神,提出了一个叫做 SIFT (Scale-invariant feature transform)的超强局部特征点:
Lowe, David G. "Distinctive image features from scale-invariant keypoints."International journal of computer vision 60.2 (2004): 91-110.
具体原理可以看上面这篇被引用 4万+ 的论文或各种博客,简单地说,这个方法提取的特征点只跟物体表面的某部分纹理有关,与光照变化、尺度变化、仿射变换、整个物体无关。
因此,利用 SIFT 特征点,可以直接在相机图像中寻找到与数据库中相同的特征点,这样,就可以确定相机中的物体是什么东西(物体识别)。

对于不会变形的物体,特征点在物体坐标系下的位置是固定的。所以,我们在获取若干点对之后,就可以直接求解出相机中物体与数据库中物体之间的单应性矩阵。
如果我们用深度相机(如Kinect)或者双目视觉方法,确定出每个特征点的 3D 位置。那么,直接求解这个 PnP 问题,就可以计算出物体在当前相机坐标系下的位姿。

当然,实际操作过程中还是有很多细节工作才可以让它真正可用的,如:先利用点云分割和欧氏距离去除背景的影响、选用特征比较稳定的物体(有时候 SIFT 也会变化)、利用贝叶斯方法加速匹配等。
而且,除了 SIFT 之外,后来又出了一大堆类似的特征点,如 SURF、ORB 等。
四. 无纹理的物体
好了,有问题的物体容易解决,那么生活中或者工业里还有很多物体是没有纹理的:

我们最容易想到的就是:是否有一种特征点,可以描述物体形状,同时具有跟 SIFT 相似的不变性?
不幸的是,据我了解,目前没有这种特征点。
所以,之前一大类方法还是采用基于模板匹配的办法,但是,对匹配的特征进行了专门选择(不只是边缘等简单特征)。
这里,我介绍一个我们实验室之前使用和重现过的算法 LineMod:
Hinterstoisser, Stefan, et al. "Multimodal templates for real-time detection of texture-less objects in heavily cluttered scenes." Computer Vision (ICCV), 2011 IEEE International Conference on. IEEE, 2011.
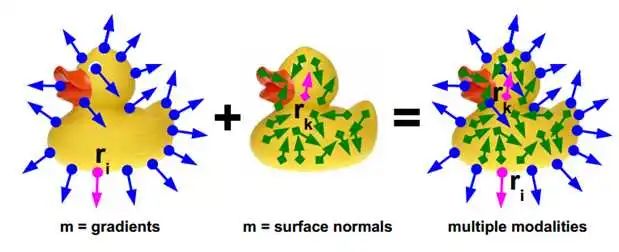
简单而言,这篇论文同时利用了彩色图像的图像梯度和深度图像的表面法向作为特征,与数据库中的模板进行匹配。
由于数据库中的模板是从一个物体的多个视角拍摄后生成的,所以这样匹配得到的物体位姿只能算是初步估计,并不精确。
但是,只要有了这个初步估计的物体位姿,我们就可以直接采用 ICP 算法(Iterative closest point)匹配物体模型与 3D 点云,从而得到物体在相机坐标系下的精确位姿。

当然,这个算法在具体实施过程中还是有很多细节的:如何建立模板、颜色梯度的表示等。另外,这种方法无法应对物体被遮挡的情况。(当然,通过降低匹配阈值,可以应对部分遮挡,但是会造成误识别)。
五.深度学习
由于深度学习在计算机视觉领域得到了非常好的效果,我们做机器人的自然也会尝试把 DL 用到机器人的物体识别中。
首先,对于物体识别,这个就可以照搬 DL 的研究成果了,各种 CNN 拿过来用就好了。在 2016 年的『亚马逊抓取大赛』中,很多队伍都采用了 DL 作为物体识别算法。
然而, 在这个比赛中,虽然很多人采用 DL 进行物体识别,但在物体位姿估计方面都还是使用比较简单、或者传统的算法。似乎并未广泛采用 DL。如 周博磊 所说,一般是采用 semantic segmentation network 在彩色图像上进行物体分割,之后,将分割出的部分点云与物体 3D 模型进行 ICP 匹配。
当然,直接用神经网络做位姿估计的工作也是有的,如这篇:
Doumanoglou, Andreas, et al. "Recovering 6d object pose and predicting next-best-view in the crowd." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016.
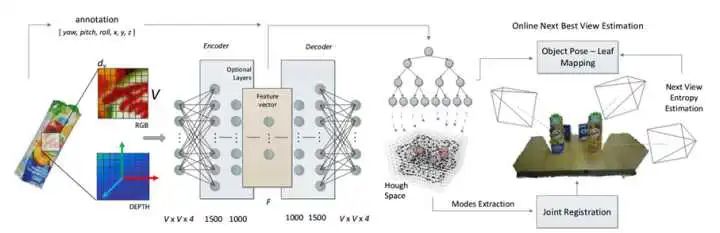
它的方法大概是这样:对于一个物体,取很多小块 RGB-D 数据(只关心一个patch,用局部特征可以应对遮挡);每小块有一个坐标(相对于物体坐标系);然后,首先用一个自编码器对数据进行降维;之后,用将降维后的特征用于训练Hough Forest。
六. 与任务/运动规划结合
这部分也是比较有意思的研究内容,由于机器视觉的目的是给机器人操作物体提供信息,所以,并不限于相机中的物体识别与定位,往往需要跟机器人的其他模块相结合。
我们让机器人从冰箱中拿一瓶『雪碧』,但是这个 『雪碧』 被『美年达』挡住了。
我们人类的做法是这样的:先把 『美年达』 移开,再去取 『雪碧』 。
所以,对于机器人来说,它需要先通过视觉确定雪碧在『美年达』后面,同时,还需要确定『美年达』这个东西是可以移开的,而不是冰箱门之类固定不可拿开的物体。