最小二乘匹配LSM，最小二乘模板匹配LSTM

2、最小二乘模板匹配

《基于序列图像》

《数字摄影测量学》

1、定义

以给定的模式作为参考模板，是高精度匹配法之一。

最小二乘影像匹配LSM：

德国Ackermann提出，利用影像窗口内的信息进行平差计算，使得影像匹配达到0.1甚至0.01像素的精度。

不仅可以解决单点匹配single-point matching求视差，也可以直接解求其空间坐标同时解求影像的方位元素；

还可以解决多点影像匹配multi-point matching和多片影像匹配问题multi-photo matching（胡翔云，2001）；

最小二乘模板匹配LSTM（least squares template matching）：

Gruen等（Gruen，1985；1992）对LSM进行了扩展，以给定的特征模式作为参考模板与实际影像做最小二乘影像匹配，从而以很高的精度提取目标，称为最小二乘模板匹配Least Squares Template Matching ,LSTM。LSTM可以扩展到利用多张重叠影像直接提取特征的物方坐标，如Gruen的LSB-Snake方法（Gruen，1997）和后续的空间圆重建等。

2、基本思想

生成一个理想的小块边缘模板；

将该模板与测量图像进行匹配，精确提取特征的边缘位置；

 

给定模板灰度f(x,y)，对应点为

测量图像的匹配窗口灰度g(x,y)，对应点为

 

模板与测量图像存在仿射变换：

 

 

 

匹配的目的是：解算出变换参数，结合 边缘点在给定模板上的精确坐标，可以得到边缘点的精确位置。

 

最小二乘是一个迭代过程，第一步的粗提取结果作为变换参数的迭代初值，代入矩阵方程求变形参数；

利用改正后的参数对测量图像重采样，计算模板与匹配子图的相关系数。若大于预定阈值，迭代结束。

3、算法

• 一般的影像匹配只考虑影像灰度的偶然误差v=g1(x,y)-g2(x,y)；而LSM在此基础上，还引入了系统变形参数，同时按照最小二乘的原则，解求这些参数。
• 影像灰度的系统变形有两类：辐射畸变、几何畸变。
• 以灰度差平方和最小为判据（灰度差v），则影像匹配方程式为
• 利用一块标准影像与待匹配影像进行最小二乘影像匹配，以期获得精确的边缘位置。

4、基于模板匹配的直线段提取（仅考虑了辐射的线性畸变的最小二乘匹配——相关系数）

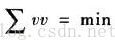
最小二乘匹配是目前常用的直线段提取的方法，该方法精度高，稳定灵活。

• 匹配前利用直线段的初始端点将影像块旋转为水平影像，水平影像每个像素都由双线性内插得到，这样可以只在断面方向匹配；
• 利用相关系数获得自适应模板：

h0,h1是辐射畸变参数。下面用g1表示实际影像模板，g2表示标准模板。

即：g1=h0+h1*g2

这里认为g1和g2是线性相关的！

 

误差：v=h0+h1*g2-g1

 

相关系数h0和h1：其中n为模板的像素数。

**************************************************************************************************************

一条直线段可用2个端点来表达，因此模板匹配的未知数就是端点坐标的改正数。由于图像已经旋转水平，那么起作用的只有y方向的改正数。（这里是不是只考虑平面上的平移和旋转，若z方向改变了，怎么办？）

• 即：误差v=gy*dy -（g2-g1）,gy是旋转到水平坐标下，y轴方向的导数，一般用梯度代替，即gy=g(i+1,j)-g(i-1,j) (i为行号，j为列号)
• 匹配时，影像窗口内每一个像元都参与平差，设直线端点i和j的坐标为（xi=0,yi=0）,(xj=Lij,yj=0),则线段上任意一点a的坐标为（xa,ya=0）
• 端点坐标的改正：
• 直线模板匹配的误差方程式：
• 对于相互遮挡的直线，需要进行消隐分析。

*************************************************************************************************************

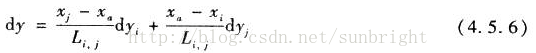
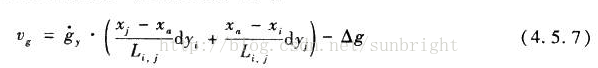
接上面的h1和h0，《数字摄影测量学》

注意：这里没有引入几何变形参数，因此，匹配算法采用目标区相对于搜索区不断移动一个整体像素，在移动的过程中计算相关系数，搜索最大相关系数的影像区作为同名像点。

搜索过程：

5、仅考虑影像相对移位的一维最小二乘匹配

灰度函数g1和g2，其中，g2相对于g1存在移位（视差值）

6、基于单点的最小二乘匹配

两个2维图像的几何变形，不仅存在如5的相对移位，图形也会变化。

考虑一次几何畸变：

再加上线性灰度畸变：