平面坐标旋转公式推导

3D坐标绕轴旋转公式推导

绕轴旋转实际上等价于平面点绕远点旋转，所以这里只用分析一下平面情况就可以。

问题转换为：平面上任意点(x,y)绕原点旋转R度后，新点坐标为多少？

一、通常情况，我们容易想到一下的推导方式（我一开始想到的），请看下图：

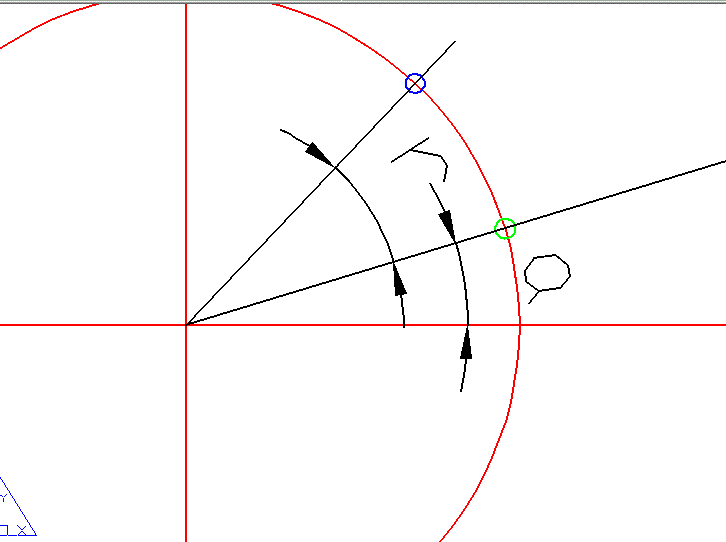
绿色的点为原始点(x,y)，转过r度后到蓝色的点的位置，我一开始想到的是先求出初始点(绿色的点)的初始角度a,然后计算出半径，根据三角关系可以得到新点的坐标。

关系式:

a=arctan(y/x)
radio=sqrt(x*x+y*y)
新点:x’=radio*Cos(a+r); y’=radio*Sin(a+r)

看起来貌似可以，但是编程处理旋转问题时发现了严重的问题，在求a的时候用了x做分母，所以就限定了x不等于0，这就不好了。

二、直角坐标系求解

思考了一天，不知道如何解决分母的问题，突然回想起来以前学过坐标变换，恍然大悟，汗一个。

还是需要通过几何关系来进行求解，可以避免定义域不连续的问题，无图无真相！

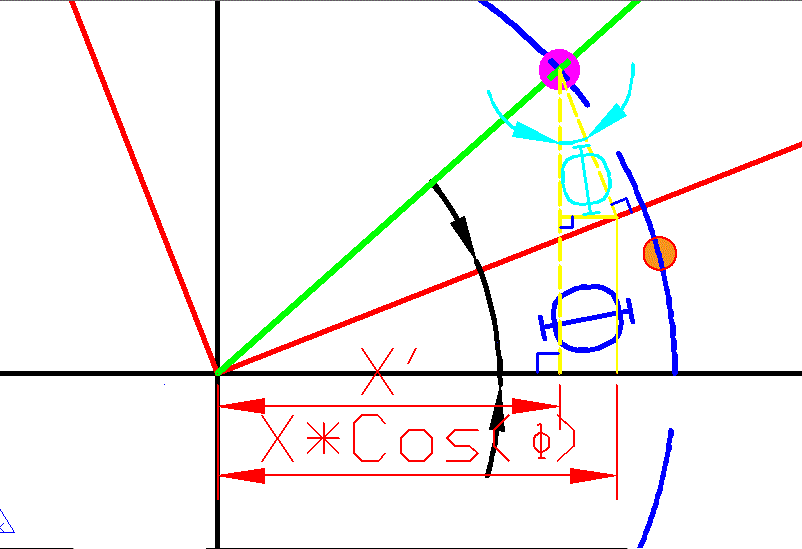
注释：图中红色的点为初始点，粉色的为新点，黑色的线为初始坐标系，红色的线为假想坐标系，黄色的线都是垂线。

在坐标变换中，我们可以换一种思考方式，点的旋转实际上可以理解为坐标系旋转到新的位置，然后求到新点相对于老坐标系的坐标即可。
图中我们很容易得到标注的两个角度相等，新点的横坐标X’等于下面尺寸标注的X*Cos(φ)-两条黄色的垂线间的距离，而这段距离我们可以在红色的新坐标系中很容易求出distance=Y * Sin(φ),所以很容易就得到了新点的横坐标

X’=X*Cos(φ)-Y*Sin(φ)          式①

同理，得到

Y’=X*Sin(φ)+Y*Cos(φ)          式②

式①和式②就是平面任一点绕原点旋转的方程。

对于3D坐标中，这便是绕Z轴旋转的公式

X’=X*Cos(φ)-Y*Sin(φ)

Y’=X*Sin(φ)+Y*Cos(φ)

Z’=Z

对于绕其他轴旋转的公式都可以用此方法得到。

三、

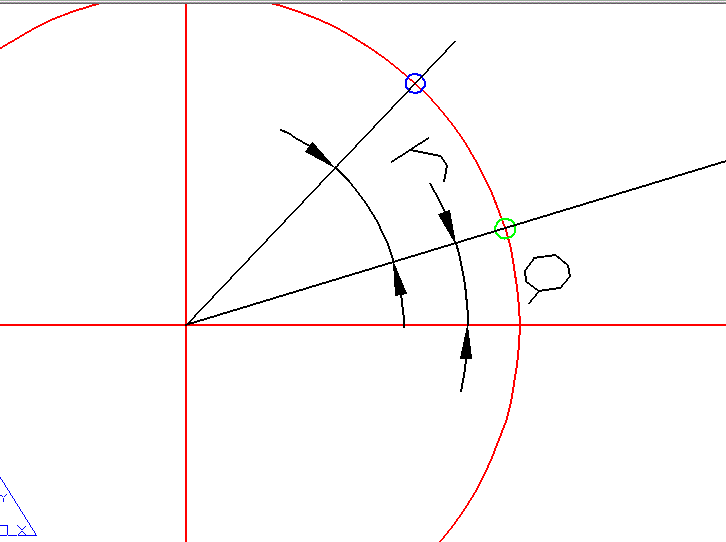
采用三角函数展开将会得到更简单的求解方法，

X'=Radio*Cos(r+a)
=Radio*(Cos( r)*Cos(a)-Sin( r)*Sin(a))
=Radio*Cos(a)*Cos( r)-Radio*Sin(a)*Sin( r)
=X*Cos( r)-Y*Sin( r)

同理得到

Y’=Radio*Sin(r+a)
=X*Sin( r)+Y*Cos( r)

看来真是要温故而知新！

坐标旋转公式

x1=cos(angle)*x-sin(angle)*y;

y1=cos(angle)*y+sin(angle)*x;

其中x，y表示物体相对于旋转点旋转angle的角度之前的坐标，x1，y1表示物体旋转angle后相对于旋转点的坐标

从数学上来说，此公式可以用来计算某个点绕另外一点旋转一定角度后的坐标，例如：A（x，y）绕B（a，b)旋转β度后的位置为C（c，d），则x，y，a，b，β，c，d有如下关系式：

1。设A点旋转前的角度为δ，则旋转(逆时针)到C点后角度为δ+β

2。求A，B两点的距离：dist1=|AB|=y/sin(δ)=x/cos(δ)

3。求C，B两点的距离：dist2=|CB|=d/sin(δ+β)=c/cos(δ+β)

4。显然dist1=dist2，设dist1=r所以：

r=x/cos(δ)=y/sin(δ)=d/sin(δ+β)=c/cos(δ+β)

5。由三角函数两角和差公式知：

sin(δ+β)=sin(δ)cos(β)+cos(δ)sin(β)

cos(δ+β)=cos(δ)cos(β)-sin(δ)sin(β)

所以得出：

c=r*cos(δ+β)=r*cos(δ)cos(β)-r*sin(δ)sin(β)=xcos(β)-ysin(β)

d=r*sin(δ+β)=r*sin(δ)cos(β)+r*cos(δ)sin(β)=ycos(β)+xsin(β)

即旋转后的坐标c，d只与旋转前的坐标x，y及旋转的角度β有关

从图中可以很容易理解出A点旋转后的C点总是在圆周上运动，圆周的半径为|AB|，利用这点就可以使物体绕圆周运动，即旋转物体。

上面公式是相对于B点坐标来的，也就是假如B点位（0,0）可以这么做。现在给出可以适合任意情况的公式：

x0 = dx * cos(β) - dy * sin(β)

y0 = dy * cos(β) + dx * sin(β)

参数解释：

x0,y0是旋转后相对于中心点的坐标，也就是原点的坐标，但不是之前点旋转后的实际坐标，还要计算一步，

β旋转角度，可以是顺时针或者逆时针。

dx是旋转前的x坐标-旋转后的x坐标

dy是旋转前的y坐标-旋转后的y坐标

x1=a+x0;

y1=b+y0;

上面才是旋转后的实际坐标，其中a，b是原点坐标

下面是上面图的公式解答：

x0=(x-a)*cos(β)-(y-b)*sin(β);

y0=(y-b)*cos(β)+(x-a)*sin(β);

x1=x0+a;

y1=y0+b;